Due piccole sfere, aventi cariche elettriche q1=+4 10^-6C e q2=+12 10^-6C rispettivamente, sono poste a 6.0 cm di distanza una dall’altra. Determinare la posizione di equilibrio di una terza carica elettrica. Ha importanza su questa posizione di equilibrio il segno della terza carica?

Dati q1= 4 10^-6C q2= 12 10^-6C d=6 cm = 6 10^-2 m Incognite Posizione di equilibrio di una terza carica q

La carica q sente una forza F1 dovuta all’interazione con la carica q1 e una forza F2 dovuta all’interazione con la carica q2. La condizione per l’equilibrio (che significa sempre Ftotale = 0) è che le due forze siano uguali come modulo e direzione, e di verso opposto. Nella situazione in esame questo si può avere solo in un punto che si trova sul segmento che ha per vertici q1 e q2. Per descrivere le posizioni la cosa più comoda da fare è di scegliere un asse di riferimento come in figura, cosicché la distanza tra q e q1 vale x e la distanza tra q e q2 vale (d-x). La condizione di equilibrio è, per i moduli delle forze, F1=F2 Þ Þ Þ se dividiamo tutto per q1 otteniamo un’equazione in cui figurano solo lunghezze, e possiamo quindi usare i cm Þ Þ e, poiché , Þ Þ Þ che ha soluzione: x=2.2 cm, vale a dire 2.2 cm da q1 e 3.8 cm da q2; l’altra soluzione x=-8.2 cm va scartata perché fuori dal segmento (lì nessuna carica sarebbe in equilibrio). Notiamo che fin dal primo passaggio abbiamo semplificato sia q che e: la posizione di equilibrio non dipende dalla carica che inserisco, e neanche dall’eventuale presenza di dielettrico.

Determinare la distanza alla quale dovrebbero porsi due elettroni affinché la forza di interazione elettrica sia uguale al loro peso sulla superficie della terra

Dati qe= 1.6 10-19 C me= 9.1 10-31 kg g= 9.8 m/s2 Incognite Distanza tra i due elettroni

Ogni elettrone sente una interazione Coulombiana repulsiva di intensità Fel., che dipende dalla distanza x dall’altro elettrone. Essendo dotato di massa sente inoltre una interazione gravitazionale attrattiva con la terra di intensità Fgrav. L’interazione gravitazionale tra i due elettroni è trascurabile (circa 1042 volte più piccola di quella con la terra) La condizione richiesta è Fgrav = Fel Þ Þ = =

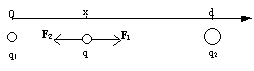
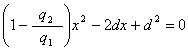
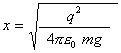torna all' indice